Forma Binomica De Un Numero Complejo Propiedades
Y las formas polares son. Multiplicación de números complejos en forma binómica.
forma binomica de un numero complejo propiedades informații importante sunt însoțite de fotografii și imagini HD provenite de pe toate site-urile web din lume. Pe această pagină avem și diverse imagini atractive în PNG, JPEG, JPG, BMP, GIF, WebP, TIFF, PSD, EPS, PCX, CDR, AI, logo, pictogramă, vector, alb-negru, transparent etc.
Vă mulțumim pentru vizită, nu uitați să marcați marcajele forma binomica de un numero complejo propiedades folosind Ctrl + D (PC) sau Comandă + D (macros). Dacă utilizați un telefon mobil, puteți utiliza și meniul paginii de salvare printr-un browser. Orice sistem de operare folosit fie Windows, Mac, iOS sau Android poate descărca imagini folosind butonul de descărcare.
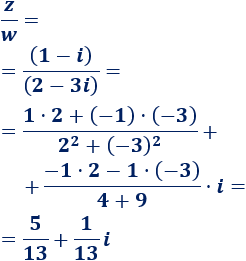Dividir Numeros Imaginarios Matematicas Faciles
Propiedades básicas de los números complejos demostraciones.
Forma binomica de un numero complejo propiedades. El número b es la parte imaginaria del número complejo. Un número complejo en forma binómica es a bi. Si a 0 el número complejo se reduce a bi y se dice que es un número imaginario puro.
Por ejemplo multiplicar y dividir complejos es más rápido en forma polar pero sumar y restar es más fácil en la forma binómica. Dado que hemos definido un número complejo como un par ordenado de números reales es natural interpretarlo como un punto del plano. Como ya hemos dicho en la forma binómica un complejo z se escribe como la suma de un número real a y un número real b multiplicado por la unidad imaginaria i.
Un número complejo en forma polar consta de dos componentes. La resta de un complejo z y de su conjugado es el doble de la parte. De hecho otra forma alternativa de representación consiste en utilizar el vector que se define entre el origen de coordenadas y el punto p denominado afijo del número complejo.
Módulo de un número complejo. La multiplicación de números complejos en forma binómica se realiza igual que la multiplicación de polinomios cuando tenemos un polinomio por un polinomio es decir se multiplica cada término del número complejo por los otros dos términos del otro número complejo ya que realmente estamos multiplicando dos binomios. El argumento principal o fase de un número complejo genérico.
Breve explicación de qué es el conjugado de un número complejo y la forma de encontrar el conjugado con operaciones como suma o resta dentro del curso de números complejos. Como el conjunto de mandelbrot pueden obtenerse a partir de propiedades de convergencia de una sucesión de números complejos. Pero además también existe lo que se llama el opuesto de un número complejo.
Cada número complejo en forma binómica a bi se representa como un punto pab en el plano complejo. El módulo del complejo z y alpha su argumento la forma trigonométrica de z es. Como podrás suponer esta no es la única forma de representarlos.
El conjunto de los números complejos se designa por. Puede observarse que para definir un número complejo tanto de esta forma como con la representación binomial se requieren dos parámetros. El módulo de un número complejo es el módulo del vector determinado por el origen de coordenadas y su afijo.
Para trabajar con el cociente hemos definido el número conjugado de un complejo. En este caso lo que cambiamos de signo no es solo la parte imaginaria como en el conjugado sino también la parte real. En algunos textos de física y de ingeniería la unidad imaginaria se designa como j para no confundir con la i que suele indicar la intensidad de corriente eléctrica.
El número a es la parte real del número complejo. Si b 0 el número complejo se reduce a un número real ya que a 0i a. En forma polar el producto y el cociente de complejos se.
Operaciones Con Numeros Complejos Trucos Y Ejercicos Resueltos
Numeros Complejos
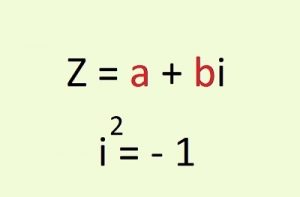Caracteristicas De Los Numeros Complejos Propiedades Ejemplos
Ejercicio 5 Potencia Y Raiz En Forma Polar Ejercicios De
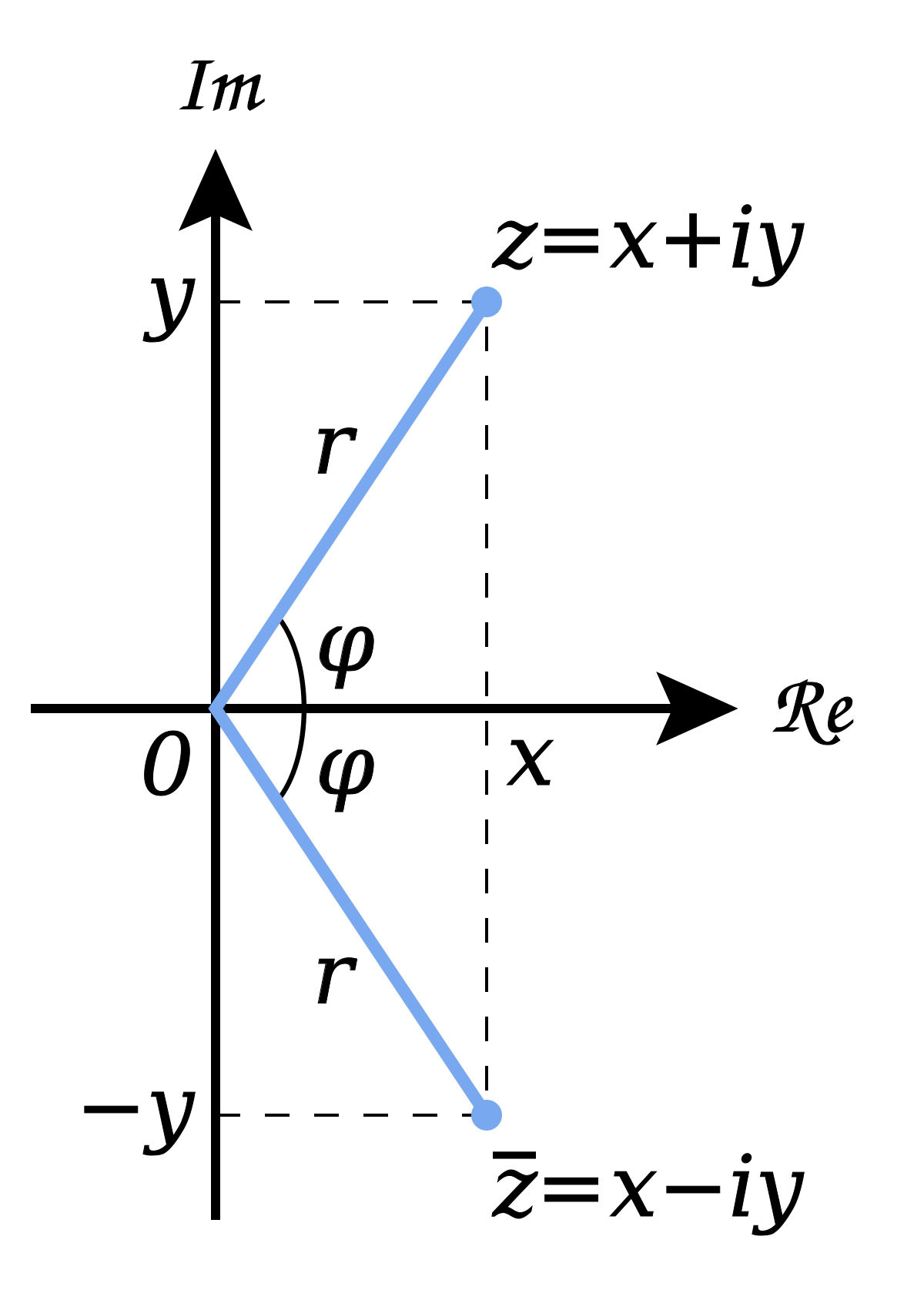Numero Complejo Wikipedia La Enciclopedia Libre
Teoria Tema 3 Complejos Definicion Y Propiedades Pdf Descargar
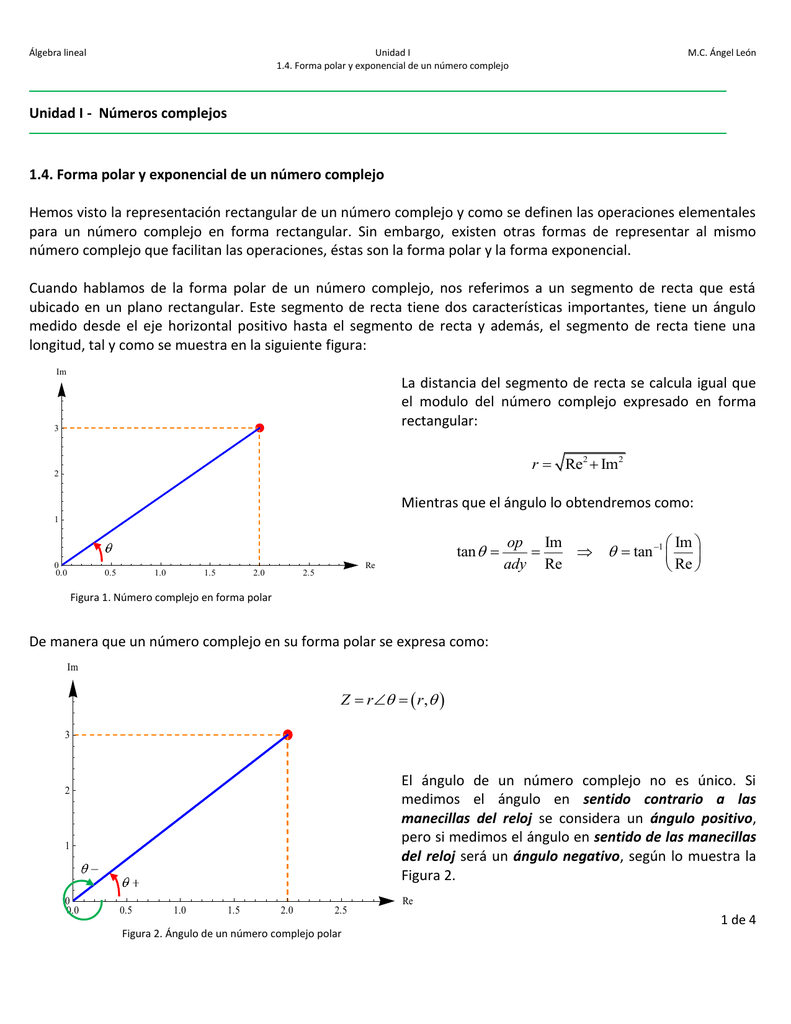Unidad I Numeros Complejos 1 4 Forma Polar Y Exponencial De Un
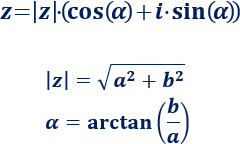Numeros Complejos O Imaginarios
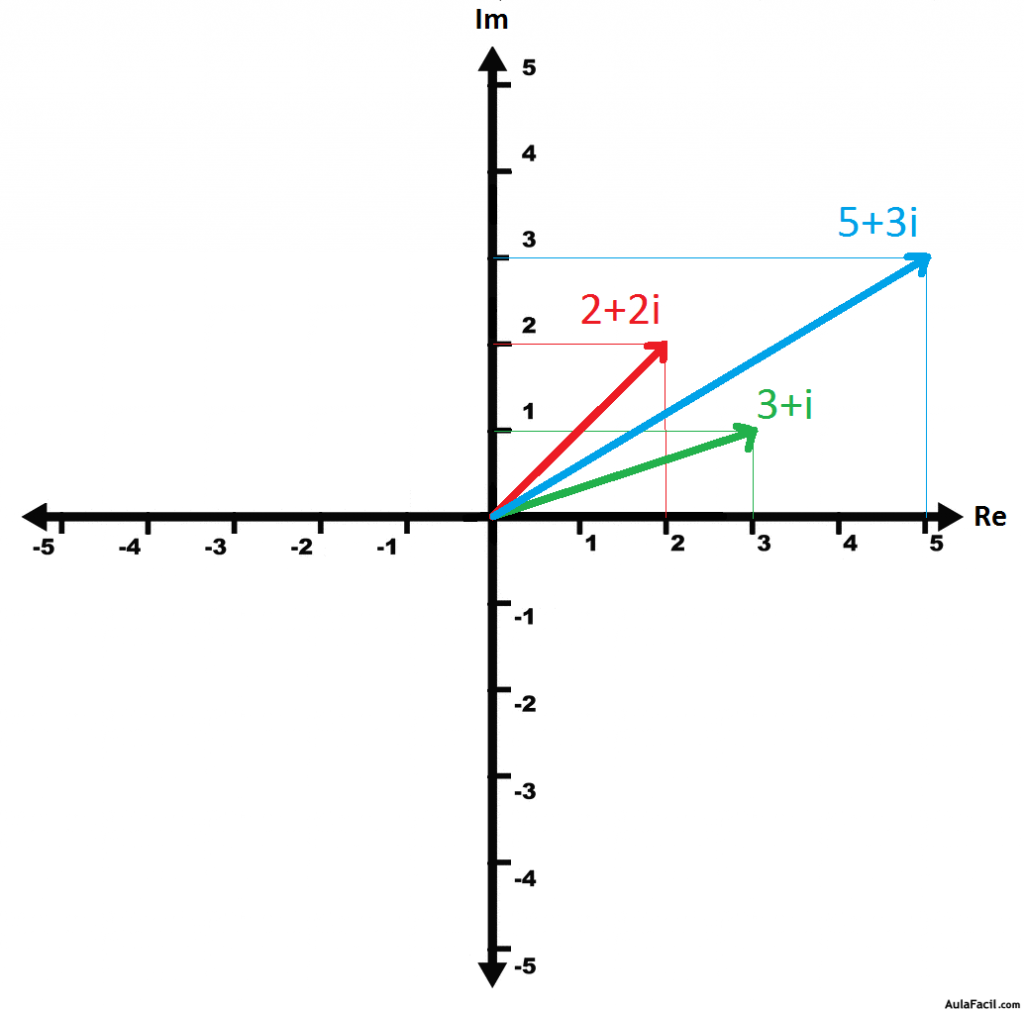Operaciones Con Numeros Complejos En Forma Binomica
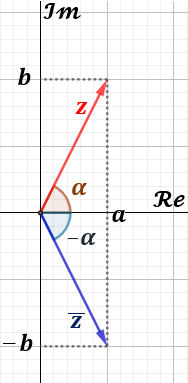Conjugado De Un Numero Imaginario Matematicas Faciles
Numeros Complejos Operaciones Ejemplos Ejercicios Resueltos
Ejercicios Resueltos De Numeros Complejos Pdf Descargar Libre
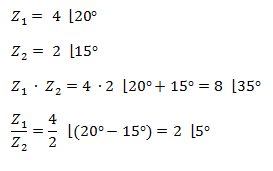Multiplicacion Y Division De Numeros Complejos Fisicapractica Com
You have just read the article entitled Forma Binomica De Un Numero Complejo Propiedades. You can also bookmark this page with the URL : https://forma-romania.blogspot.com/2017/07/forma-binomica-de-un-numero-complejo.html?m=1
Belum ada Komentar untuk "Forma Binomica De Un Numero Complejo Propiedades"
Posting Komentar